当サイトの概要とページの一覧
[mathjax]
このページでは、当サイト「ルールとパターン」の概要と、サイト内のページ一覧のリストを載せています。
当サイトの概要
当サイト「ルールとパターン」では、実際に私がプログラミングで描いた画像を紹介していきます。
プログラミングでどのように図形を描くのか、ここで少しだけ解説します。
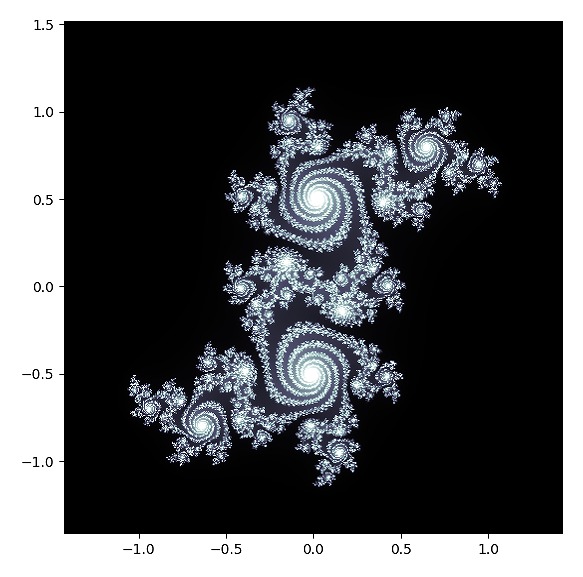
例えば下図のマンデルブロ集合の図は一本の式を基に描いています。
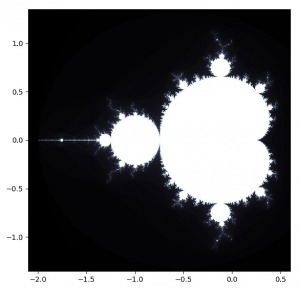
使用した式は
$$Z_{n+1}=Z_n^2+C$$
というものです。
描き方ですが、まず描画するフィールドを細かく分割しておきます。
そして分割した各点の座標で上の式を何度も計算し、計算した値によってその点の色を決めていきます。
ちなみに、分割する点の数は150万点以上にもなります。
さらにその点ごとに100回近く先ほどの式を計算しなければいけません。
この作業は人力ではとても終わりません。
それを可能にしてくれるのがコンピュータによるプログラミングです。
プログラミングによって、この合計1億回以上の計算もほんの数秒で終わります。
コンピューター様様です。
この模様(パターン)は、数式などの規則(ルール)によって描かれています。
そこで、このサイトを「ルールとパターン」という名前にしました。
式を使って描いた模様にはいろいろな特徴があり、私はそこに強く惹かれます。
特徴の一つは対称性を持っていることです。
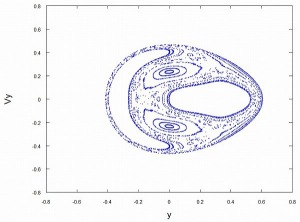
線対称であったり点対称であったりとパターンによって様々ですが、ルールに沿って形作られた図形には対称性が備わります。
このきっちりとした対称性に美しさを感じるのが、パターンに惹かれる理由の一つです。
ところで、私が勝手に"複素数平面の海"という名前を付けたパターンがあります。
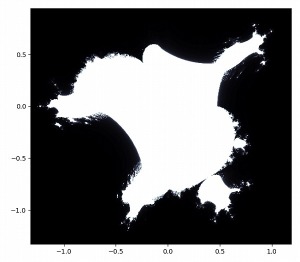
このパターンはマンデルブロ集合と同じような式で描くことができます。
複素数平面の海を拡大していくと多種多様なパターンが現れます。

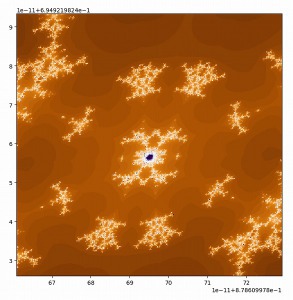
複素数平面の海のパターンたちは、一見対称な形をしています。
ところが、よくよく見ると歪んでいたり細部が違っていたりするため、実は対称ではないようです。
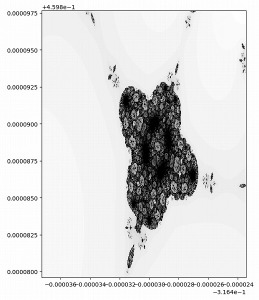
この対称性に歪みが加わったパターンも趣があり、とても美しく感じます。
マンデルブロ集合や複素数平面の海には、拡大しても終わりがないという特徴もあります。
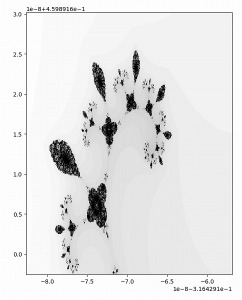
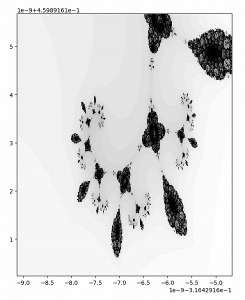
パターンを拡大していくと同じような模様が現れ続けます。
10のマイナス15乗の大きさまで拡大してみましたが、パターンに終わりは来ませんでした。
おそらく無限に終わりが来ないのだと思います。
この無限に拡大していけるというのは、人間が捉えるには難しい感覚です。
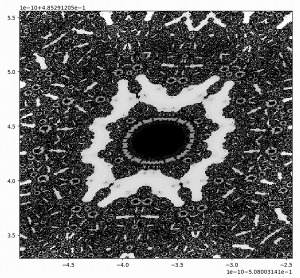
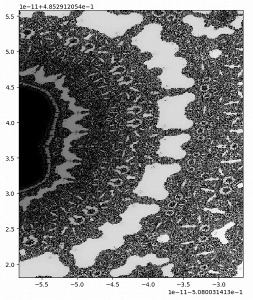
模様が模様によって形作られ、それが無限に続いていきます。
その無限に続くという全く理解できない性質が、とても刺激的で心を揺さぶられます。
そこにもルールで作ったパターンの魅力があります。
長くなりましたが、当サイトではこのような魅力的で怪しいパターンたちを紹介していきます。
かなりニッチな内容だと思いますが、同好の士がいることを願い、また、こういったものに興味のなかった方が一人でも興味を持っていただけるよう、更新をしていきたいと思います。
宜しくお願い致します。
ページ一覧
当サイト内のページ一覧です。
マンデルブロ集合
バーニングシップフラクタル
複素数平面の海
ジュリア集合
漸化式
極座標
エノン・ハイレスポテンシャルのポアンカレ断面
エノン・ハイレス(henon-heiles)ポテンシャルのポアンカレ断面図
いくつかのエネルギーでのエノン・ハイレスポテンシャルのポアンカレ断面図
理論と描き方
マンデルブロ集合の図を理解するための基礎知識・虚数と複素数について
マンデルブロ集合の図を理解するための基礎知識・複素数の演算について
当サイトについて