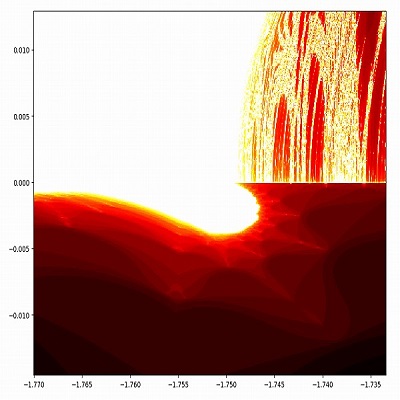
複素数平面の海5・くびれ部分の拡大
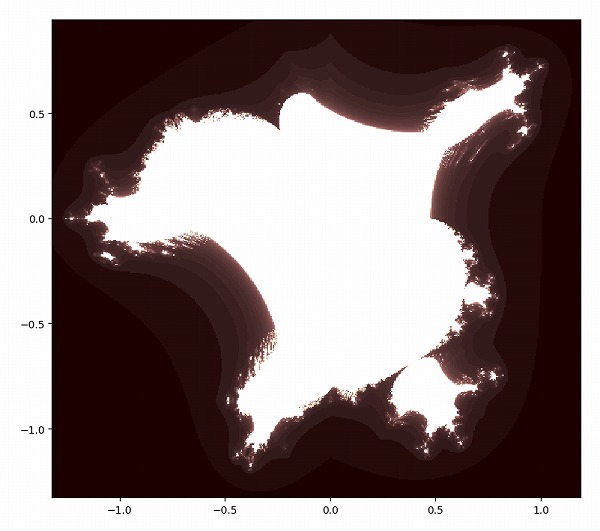
パターンのくびれ部分を拡大してみましょう。

右側の淵の一部を拡大します。
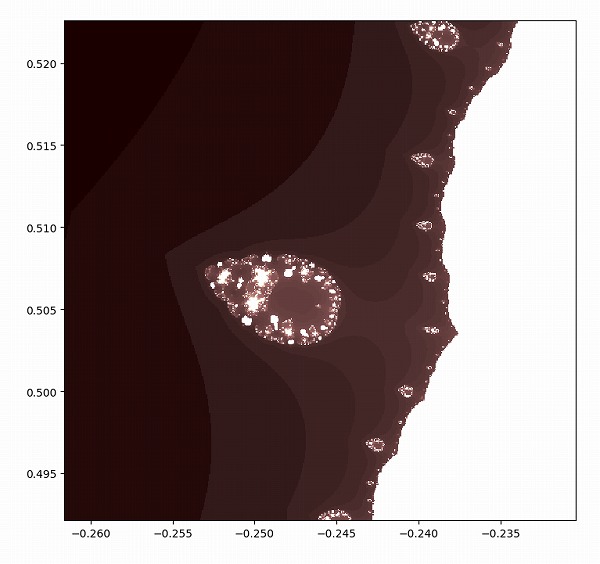
また面白い模様が見えてきました。
さらに淵の近くを拡大します。
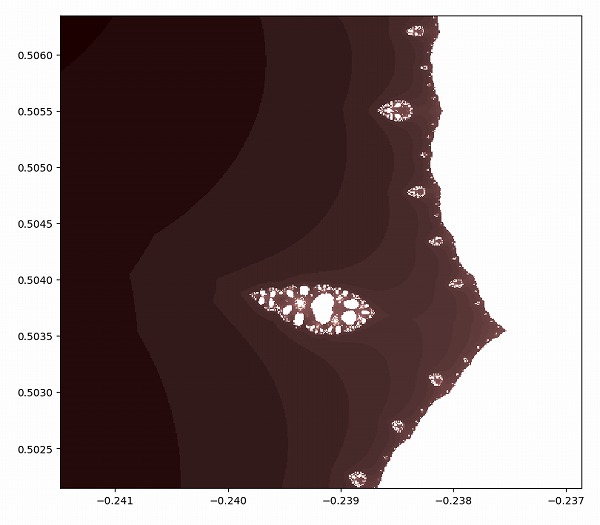
微生物のように見えるパターンです。
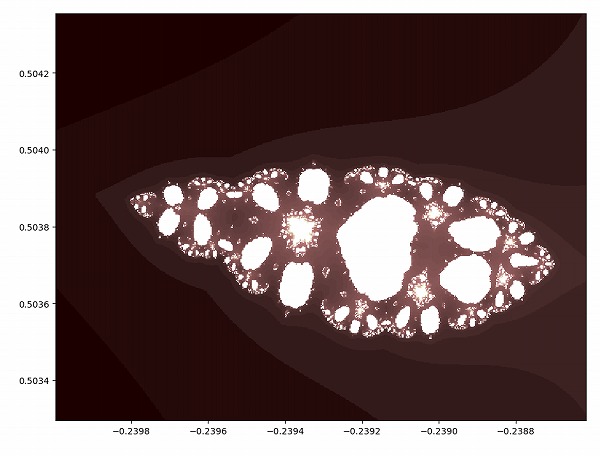
下側を拡大してみます。

下側の真ん中にある、四角形に近い白い部分を拡大します。
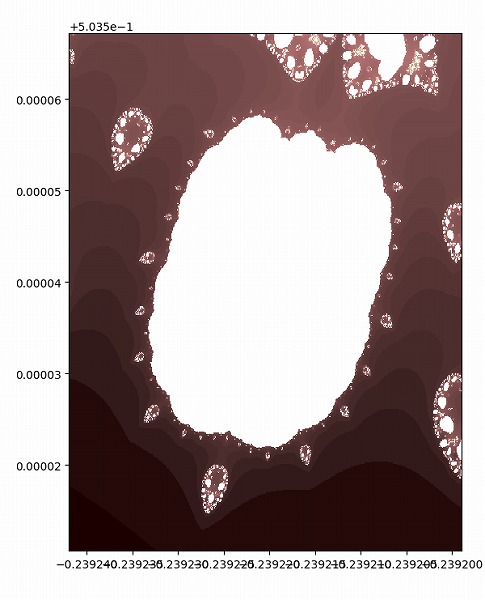
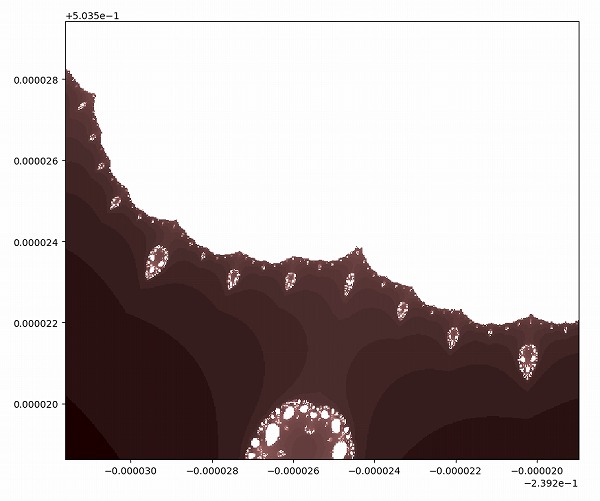
下の物体の中にある、小さい三日月形を拡大します。
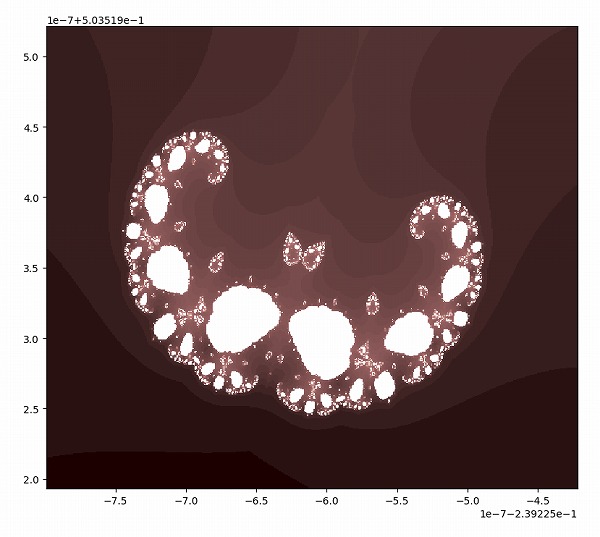
右側の丸まっている部分を拡大します。
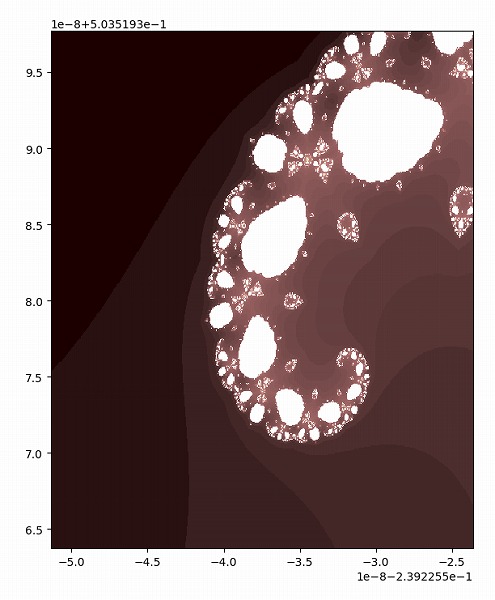
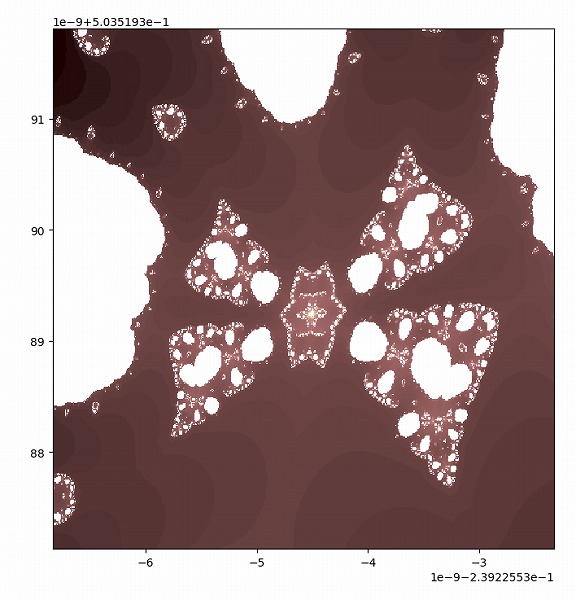
まるで蝶かリボンのようなパターンです。
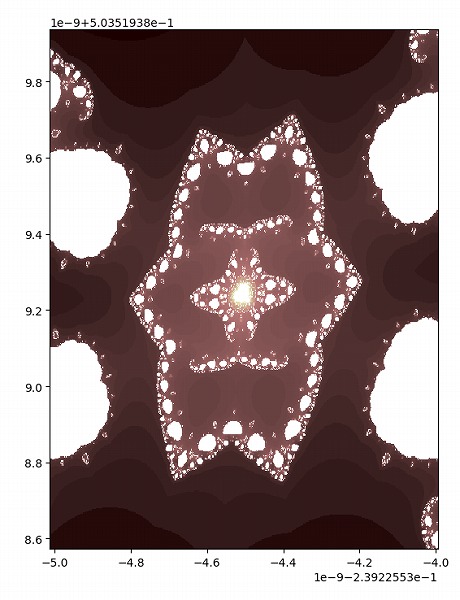
真ん中には星が隠れていました。

さらに中心には全体図と同じようなパターンがあります。

マンデルブロ集合やバーニングシップフラクタル、そしてこの複素数平面の海などのパターンは、拡大していくと同じような形が現れ続けます。
同じような形でありながら、少しづつ角度や周囲の位置関係が違っていたりして、全く同じようなパターンが現れるのは見たことがありません。
さらに拡大していくと、無限に形の違うパターンが現れ続けていくのでしょうか。
感覚では理解できないような、この無限性とでもいうべきパターンの存在が、私が複素数平面の図形に惹かれる理由です。